練習問題5 3 g が得られました。 このとき、誤差の絶対値は何g以下になるか答えなさい。 <<L47 代表値平均値・階級値 の問題に戻る L48 近似値・有効数字 の解答表示>> 中1数学・練習問題一覧 中2数学・練習問題一覧 中3数学・練習問題一覧 近似値の求め方計算問題 ここでは、一次近似の考え方で近似式や近似値を求める問題を解いてみましょう。 計算問題①「\(\sqrt4{80}\) の近似値」精度保証付き近似解法 最大化問題 OPT 最適値 Obj アルゴリズムで得られる目的関数値 OPT/Obj このアルゴリズムの どんな問題例に対しても,OPT/Obj ≤ αを満たすとき,このアルゴ リズムを という. 最小化問題に対しては,Obj/OPT≤ αを満たすαで評価する. 5 章(組合せ最適化問題) 近似解法

中学数学 近似値 有効数字 から誤差を求める1つの方法 Qikeru 学びを楽しくわかりやすく
近似値 問題
近似値 問題-Excelで点の幅01刻み程度の散布図(A列に−05~05,B列に= (1a1)^ (1/4)など)を描き,近似曲線:線形近似を追加する 式そのものを入力しているのでなく,粗雑な点を並べているだけなので,式の係数は「完全には一致しない」が,そこそこ合う(以下の問題も同様) →解答を隠す← (3) x がほぼ 2 に近い値であるとき, の近似式を x の1次式で表してください. 解答より複雑な問題では,すべての境界条件を満たす近似関数を 探すのが困難な場合が普通であり,このままでは弱形式は 使えそうもない。 また,近似関数は4階の微係数が定義できるものでないといけなかったことも 思い出して欲しい。 これを改善するためには境界条件の誤差も含めた 弱形式を定義し直せばよく,同時に近似関数の微係数の階数も 小さくできれば




近似値の問題です 教えて下さい Clear
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru取材や仕事等の 近似値を求める問題 √2=1414 √3=1732とした場合、次の問いに答えなさい。 √300=√100×√3 =10×1732 =1732 こういった問題なら解けるのですが次の問題の解き方が分かりません。解き方を教えてください。 √小規模固有値問題: Arnoldi(M,W,G) 法 近似固有対の構築 初期ベクトル 部分空間 の構築 近似固有対 の構築 収束判定 Arnoldi 法の拡張 9 のとき, Arnoldi(M,W,G) 法 従来法では,基底生成毎に or の計算が必要 解法 a Neumann級数展開 # 逆行列( )の近似 解法 b Krylov部分空間法 解法 c 定常反復法 # ベ
平方根(ルート)の近似値の求め方 √2≒141 というのは聞いたことがありますか? 平方根を、近い大きさの数である「近似値」で表せ、という問題はよく出題されます。ここではこの、「平方根の近似値」について説明します。 覚えるべき近似値一問ずつ丁寧な解説がついているから安心。問題を分野別一覧で見れば傾向と対策ができます。 午前分野別 午後分野別 キーワード索引 令和元年秋午前 令和元年秋午後 平成23年 春期 基本情報技術者 午前 問02 問02 相対誤差 三つの実数 x ~ z とそれぞれの近似値が次の場合,相対誤差2階導関数にも前進差分、後退差分の近似があり、それらはそれぞれu(x2h) やu(x 2h) をu(x h) やu(xh) の代わりに用いることで導出できる。 問1 2階導関数について、2次の前進差分、後退差分近似を求めてみよ。 13 境界値問題 さて本題の境界値問題に戻ろう。
くり、それを解いて近似解を求める方法である。差分法は、微分方程式の初期値問題や境 界値問題の解を、近似的に解く手法として計算機が登場した当初から利用されており、数 値計算の安定性、数値解の誤差評価などに関する多くの研究があるが、それらはまだ十分 とは言えず、計算コスト乗法・除法/平方根の近似値/加法・減法/加減乗除全般/式の値/ 平方根の応用(√が整数) /平方根の応用(整数部分・小数部分)/平方根の応用(その他)/ FdData 中間期末製品版のご案内 FdData 中間期末ホームページ 掲載のpdf ファイル(サンプル)一覧 ※次のリンクはShiftキーをおしながら近似値 (きんじち)とは、必要とされる 誤差 の範囲内で、ある 数 を表していると思って構わない数値のこと。




無料 中3数学 発展 応用問題 問題プリント 314 平方根6 いろいろな計算1




高校数学 近似値の計算 問題編 映像授業のtry It トライイット
Du dx ¶ = 0 fi0u(a)fi1u0(a) = fi fl0u(b)fl1u0(b) = fl に対しSW近似とPearson近似を併用すれば、差近似値 近似値とは 真の値に対して、真の値ではないがそれに近い値を近似値という。 測定値や四捨五入して得られた数字は近似値である。 誤差 近似値と真の値の差を誤差という。 誤差=近似値ー真「近似値」の問題では、 分母は100にする方がよいです。 √100 = 10 が使えるからですね! これを知っておくと 計算が速いですよ。 中3数学の大事なコツです。 「0.2 を直すときに、 分母を100にすると なぜ分子が になるのですか?」 と思う中学生は、




中1数学 近似値 練習編 映像授業のtry It トライイット




近似値と有効数字 の問題のわからないを5分で解決 映像授業のtry It トライイット
Log101とlog0998の近似値を求める問題です。 対数関数,指数関数,無理関数などで表された値が求めにくいとき, 1次近似式 が活躍します。 例えば,log101の場合, log101=log (1001) と見ます。 すると,f (x)=logxにおける1次近似式が使える形になります。 POINT 実際に,log101とlog0998の近似値を求めていきましょう。 近似値・誤差の練習問題です。 最近少しずつ入試でも出題され始めたところであります。 練習を重ねて習得していきましょう。 近似値・誤差 近似値と誤差真の値に近い値を近似値、近似値と真の値との差を誤差といいます。 (誤差)=(近似値)-(真の値) 有効数字近似値を表す数字のうち、信頼できる数字を有効数字といいます。 近似値の「これを使いなさい」と近似値が 与えられる問題のことですね。 結論から言えば、 「 √2」「 √」に変形すると、 求めることができますよ。 ( などの形です。) 中3数学の大事な問題なので、 しっかり解説していきますね。 まずは準備体操を! ご質問の問題を解くには、



平方根の近似値 この問題の意味が分かりません そもそも数字の並び Yahoo 知恵袋




中3数学 平方根の近似値を求める問題 5分で学習 Youtube
近似値と誤差 測定結果や四捨五入によって得られた値のように、正確な値に近い値のことを 近似値 と呼ぶ。 375の小数第2位を四捨五入すると38この値を近似値という。 近似値から正確な値を引いたものを 誤差 と呼ぶ。 38―375=005 では問題です。 ある数aの少数第2位を四捨五入したところ43になった。 次の問いに答えましょう。 (1)aの値の範囲を ≦a<という不等式で求めることができます。 近似値と実際の値との差、つまり「近似値実際の値」の事を誤差と言います。 近似値が小数第一位で四捨五入した04、実際の値がであれば 誤差== 実際の値から小さいということが分かりやすいですね。 では小数第一で四捨五入した近似値が1の場合、誤差の絶対値は最大でいくつ 計算方法や求め方、近似値の覚え方、利用問題 21年2月19日 この記事では「平方根」について、その性質や計算方法などをできるだけわかりやすく解説していきます。 また、平方根の近似値の覚え方や実際の問題なども紹介していきますので、この記事を




中学数学 近似値 有効数字 から誤差を求める1つの方法 Qikeru 学びを楽しくわかりやすく




中3数学 平方根の近似値 Youtube
点境界値問題に対し差分近似の打ち切り誤差が1次であっても差分解が2次の精度をもつ 事例が見出され、1986年MantauffelWhiteによってDirichlet境界条件を含む混合型2点 境界値問題 ¡ d dx µ p(x) du dx ¶ f µ x;u;11 対象とする問題 近似 先の問いであげたnp 困難な最適化問題それぞれについて,解の値 が何であるのかを示し なさい. 定義12 p を任意の(np困難な)最適化問題とする.i をp の任意の入力とする.このとき,i の 最適解をopt(i) と表記する. 例12 独立頂点集合問題であれば,opt(g) は近似値、誤差、有効数字の意味を学び、その求め方、表し方を練習する問題プリントです。 近似値と有効数字 (1) 答え



至急明日テストです 中三数学の近似値の問題です 3 の解き方って Yahoo 知恵袋




近似式とは 練習問題で微分の応用を理解しよう 高校生向け受験応援メディア 受験のミカタ
近似値と誤差の考察 The Consideration of と一致しているか否かの問題は,この裏値に対す る近似値の誤差の限界をみることによってのみ知 り得る。 .了 たとえば,ポこ1.・日を某値としたと き,瓜=1.-なる近似値は,誤差の限界が, 1血≦10‾4!2で押えられるから,この近似一問ずつ丁寧な解説がついているから安心。問題を分野別一覧で見れば傾向と対策ができます。 午前分野別 午後分野別 キーワード索引 令和元年秋午前 令和元年秋午後 平成年 春期 基本情報技術者 午前 問06 問06 ニュートン法に関する記述 方程式 f (x ) = 0 の解の近似値を求める 練習問題 以上、平方根の近似値問題のやり方を2とおり解説しました。 ≪基本のやり方≫ ルートの中が自然数→ルートを簡単にする! ルートの中が小数→分数になおして有理化! ≪ラクなやり方≫ 「100」を見つける!
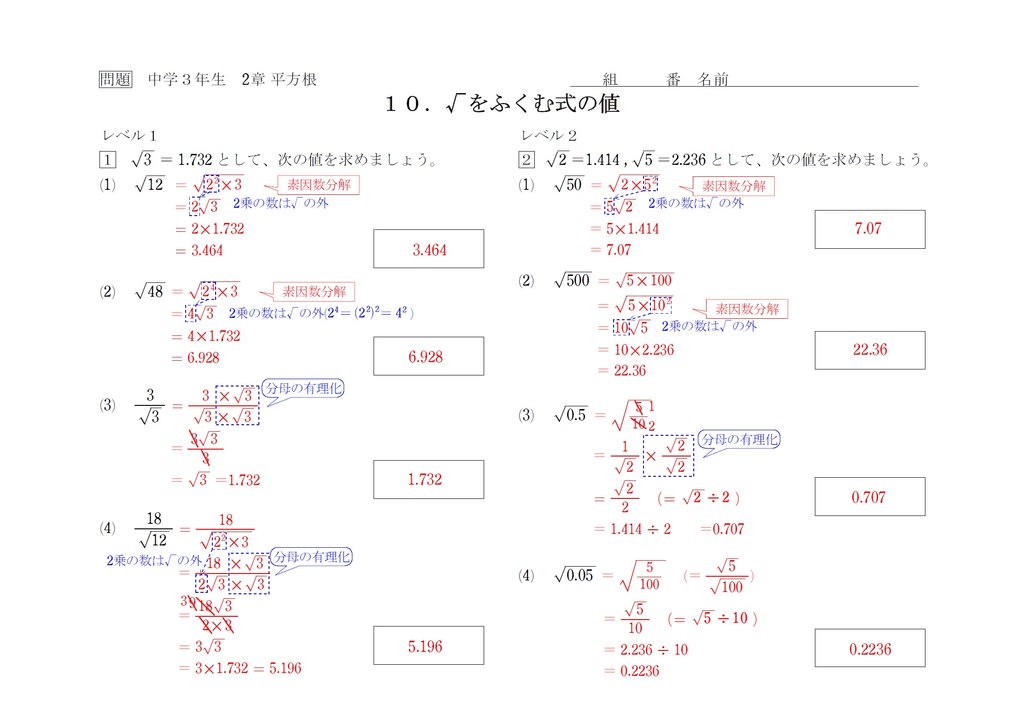



中3 平方根10 近似値 中学数学の勉強に



17年06月の記事 中学数学高校数学個別指導in山形市 数専ゼミ
近似値と有効数字 本時の目標 近似値、真の値、誤差の意味を理解する。 有効数字の意味と表し方を理解し、測定値を有効数字で表すことができる。 ※問題は、略案で創る中学校数学科の授業より引用 もちろん近似値ですので実際の値とはずれがありますが、hが小さければ、それなりに精度の良い近似が可能です。 2.近似式の練習問題を使って解説! 問1: h ≒ 0のとき、sin(ah) の1次近似を利用して、sin31°の近似値を求めよ。 解答・解説: 近似値を利用した計算は、三角関数や対数関ここでは,目的関数の値を最小化する最適化問題を考える. 最適化問題Pに対して, S 実行可能解 評価値val(S) Opt 最適解 評価値val(Opt) 近似率(近似性能)δ= val(S) / val(Opt) (最大化問題の場合にはval(Opt) / val(S)と定義 δ近似アルゴリズム=近似率δ以下の解を




近似式とは 練習問題で微分の応用を理解しよう 高校生向け受験応援メディア 受験のミカタ



服部嗣雄 難問題の系統とその解き方 新課程 物理 の活用法と歴史
無理数の近似値の求め方 標準偏差を求める問題の解答の最後に, √4=142 とあるのですが,なぜそのようになるのかわかりません。 進研ゼミからの回答! こんにちは。 いただいた質問について,さっそく回答させていただきます。 近似値と誤差の練習問題1 ある数xの1の位を四捨五入すると0になった。このとき次の問いに答えよ。 (1)xの値の範囲を、不等号を使って表しなさい。 (2)誤差の絶対値は大きくてもどのくらいと考えられるか。 近似値と誤差の解答1 問題1.次の値は四捨五入によって得られた近似値である。真の値を $a$ とするとき、$a$ の範囲を不等式で表しなさい。 (1) $58 \ (\mathrm{kg})$ (2) $172 \ (\mathrm{cm})$ (3) $29 \ (\mathrm{km})$ (4) $17×10^2 \ (\mathrm{cm})$




中3数学 平方根 近似値と有効数字 解説 Youtube



しな鉄クイズ 問題
近似値・有効数字 誤差と有効数字、近似値の表し方の問題です。 高校の理科でも使う分野なので、教科書でしっかり意味を確認してから問題に取り組んでください。 誤差 とは、真の値と近似値との間にある違い、つまり、 誤差=近似値-真の値 です。 例)測定値 505kg 真の値 502kg のとき 505kgー502kg=03kgが誤差になる。 よく出る問題 ある数aの小数第解析学において、ピカールの逐次近似法(ピカールのちくじきんじほう、英 Picard iteration )とは、常微分方程式の初期値問題に対し、解に一様収束する関数列を構成する手法 。 常微分方程式の初期値問題と同値な積分方程式に基づき、関数列を逐次的に構成する。近似アルゴリズムに対するアプローチ 上限の研究 ・問題に対する、c近似アルゴリズムを開発する。 ・cの値を小さくしていく方向。 下限の研究 c近似アルゴリズムを 持たないことを示す。 ・cの値を大きくしていく方向。 例:MAX 3SAT ・上限:8/7近似



平方根の近似値を有効数字3桁で求めろという問題なのですが それぞれどう求めたら Yahoo 知恵袋




近似値を概数を使って求める場合です 下の問題で何でsin61 じゃなく Okwave
近似値1 名前 ある品物を1g単位で測れるはかりで測ったら gありました。 ①この品物の真の重さをagとするとき、aの値の範囲を 不等号を使って表しなさい。 ②誤差の絶対値は大きくてもどのくらいと考えられるか。熊本大学数理科学総合教育センター 中心極限定理と正規近似 問題1 解答 1 コンピュータを使い0 から10 までの実数を, 一様分布に従うものとしてランダムに300 個 生成した (1) 中心極限定理を用いて, 生成した実数の平均が近似的に従う正規分布を求めよ (2) (1) で求めた近似正規分布を用いて3次の値を有効数字が3けたの近似値とするとき,有効数字がはっきりわかる形で表しなさい。 (1)1870g (2)500mL (3)2750m n 1ア,測定値 イ,真の値 ウ,近似値 エ,誤差 オ,有効数字 カ,1けた キ,累乗(何乗か) 5 m L) 3(m) n 組 番 名前 12地点間の距離を測定し,10 m未満を四捨五入して




近似式とは 練習問題で微分の応用を理解しよう 高校生向け受験応援メディア 受験のミカタ



数学問題の出題範囲詳細
近似値 きんじち approximate value 真の値すなわち正しい値そのものが算出できないとき,あるいは算出できてもそれほど精密な値を必要としない場合に,その代りとして使用される,真の値に近い数値のことを,近似値という。 たとえば は円周率 π の近似値,2718は自然対数の底 e の近似
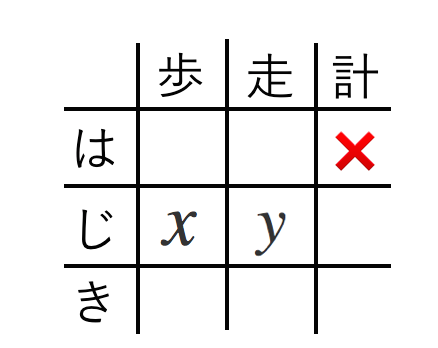



近似値の問題 苦手な数学を簡単に



近似式 京極一樹の数学塾




近似値から真の値の範囲を求める 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信



Q Tbn And9gcrxte7kpw Prbp1ha Goiskrvwgvrgwheflvtt1dxkyal9yqqhz Usqp Cau




中1数学 有効数字 近似値と誤差の要点と定期テスト対策問題 Examee
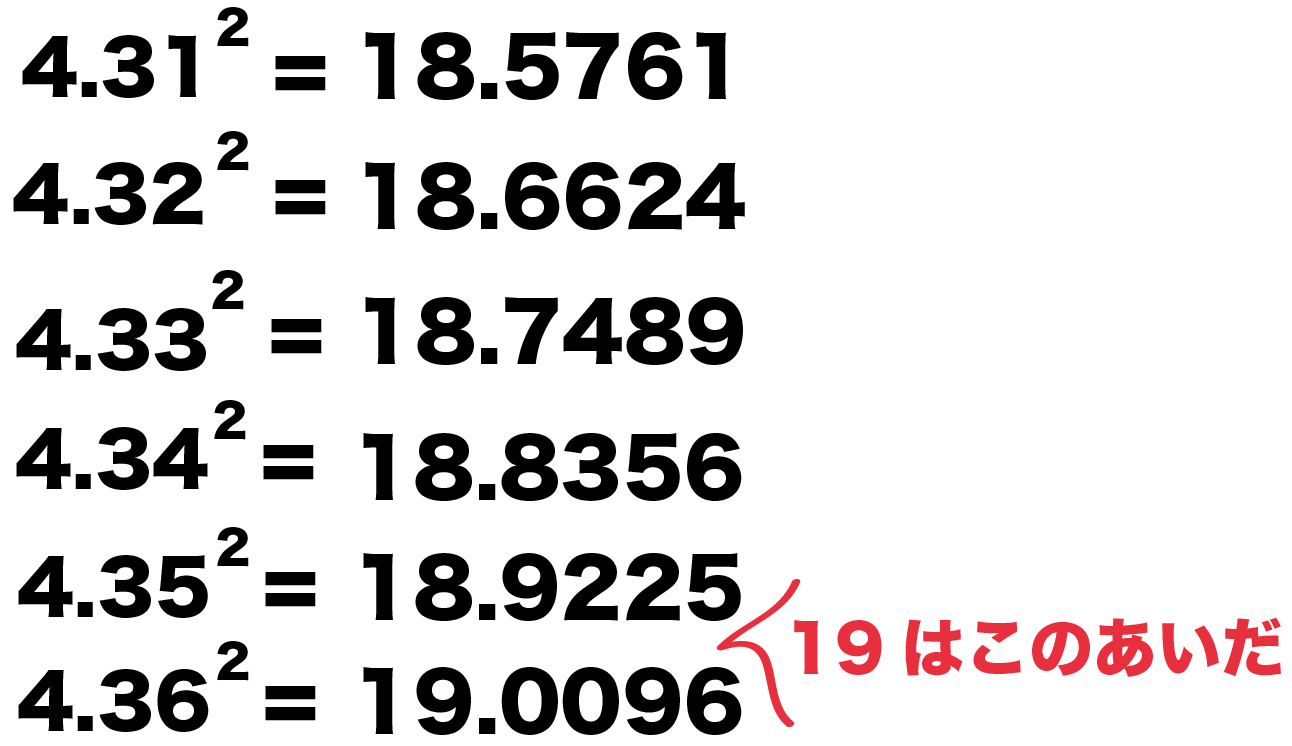



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




高校数学 対数log Abの近似値求め方 評価の方法 受験の月




近似値と有効値 数学の要点まとめ 練習問題一覧




平方根 近似値を求める 苦手な数学を簡単に




平方根の近似値 無料で使える中学学習プリント




中1 数学 近似値と有効数字 中学生 数学のノート Clear




中3数学 平方根の近似値の問題です Clear




近似値と有効数字 教遊者




近似値 有効数字 無料で使える中学学習プリント



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




近似式とは 練習問題で微分の応用を理解しよう 高校生向け受験応援メディア 受験のミカタ




中学数学 平方根 のコツ 平方根の近似値 式の値



中1数学 基本 基礎問題 資料の活用2 近似値 145




世界一わかりやすい数学問題集中1 7章 資料の活用




平方根の近似値 無料で使える中学学習プリント



無料 中1数学 標準問題 解答プリント 145 資料の活用2 近似値




近似値から真の値の範囲を求める 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信




中学1年生 数学 資料の活用 近似値と有効数字 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



次の数はいずれも少数第二位を四捨五入して得られた近似値です 真の値はどの範囲に Yahoo 知恵袋




近似値の問題です 教えて下さい Clear



1




中学数学 近似値 有効数字 から誤差を求める1つの方法 Qikeru 学びを楽しくわかりやすく




近似値と誤差とは 中学1年数学 Youtube
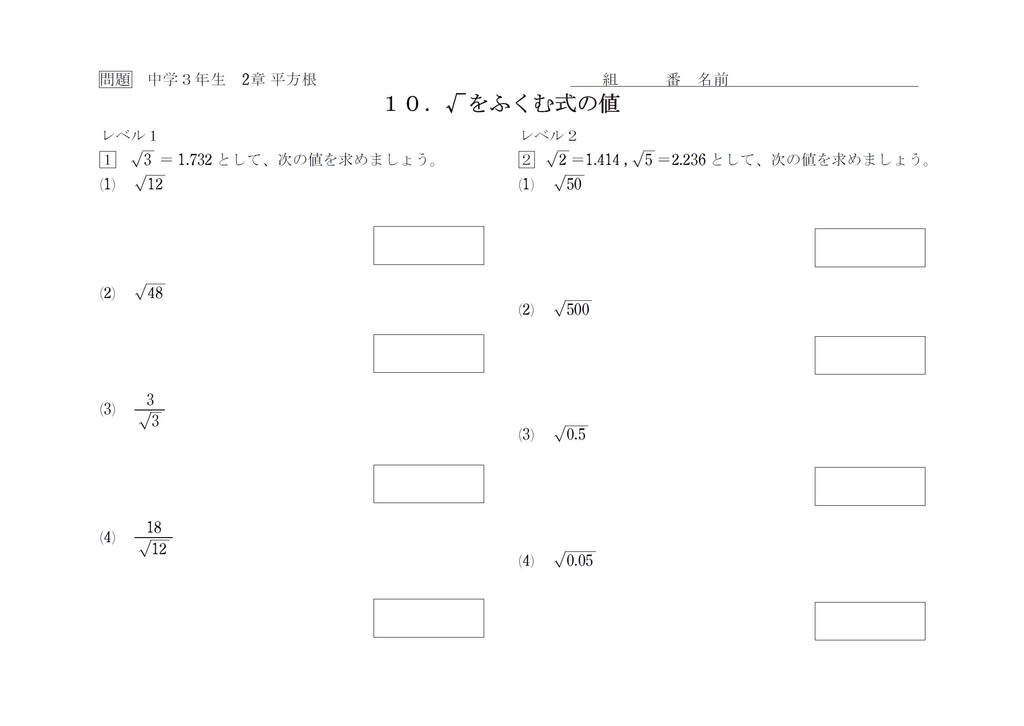



中3 平方根10 近似値 中学数学の勉強に



近似値の問題です 孤度法で解いたものと度数法で解いたもので違いが出てき Yahoo 知恵袋
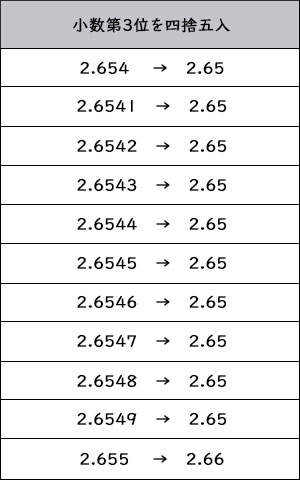



中学校1年生数学 近似値 長野地区 Itto個別指導学院 長野市の学習塾



1




中学1年生 数学 資料の活用 近似値と有効数字 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



服部嗣雄 難問題の系統とその解き方 新課程 物理 の活用法と歴史




中1 21 4 近似値と誤差 有効数字 Youtube




中学1年生 数学 資料の活用 近似値と有効数字 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




東大音ゲーサークルb4ut V Twitter 解答用紙はこちらです 近似値問題に配点はありません 同点の受験者が存在した場合に 近似値問題の数値がより正解に近い方を成績上位としました




中1数学 近似値 練習編 映像授業のtry It トライイット




中学1年の数学 動画 近似値の問題 19ch



無料 中1数学 基本解説 問題プリント 資料の活用2 近似値 145




近似値と有効値 数学の要点まとめ 練習問題一覧




中3数学 平方根 近似値と有効数字 問題 Youtube



平方根とは 計算方法や求め方 近似値の覚え方 利用問題 受験辞典




中3数学 真の値と近似値の定期テスト過去問分析問題 Atstudier




近似値と有効数字 教遊者
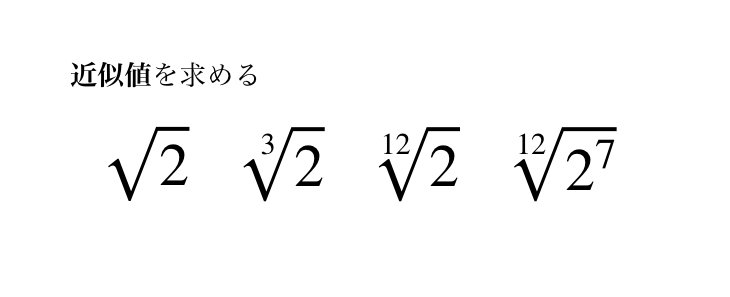



2の12乗根の近似値を求める方法を考える 鈴華書記 Note




データの分析 無理数の近似値の求め方 数学 定期テスト対策サイト




中1 数学 資料の整理7 近似値とは 13分 Youtube




数学 近似式まとめ 各種公式 求め方 理系ラボ




中1数学 近似値と誤差の求め方の定期テスト予想問題 Pikuu




近似値の問題 苦手な数学を簡単に




中3 平方根10 近似値 中学数学の勉強に



無料 中1数学 基本問題 解答プリント 資料の活用2 近似値 145



近似式 京極一樹の数学塾




近似値と有効数字 Youtube




中学数学 近似値 有効数字 から誤差を求める1つの方法 Qikeru 学びを楽しくわかりやすく




中学数学3年 平方根とその近似値 大小 有理数と無理数 受験の月
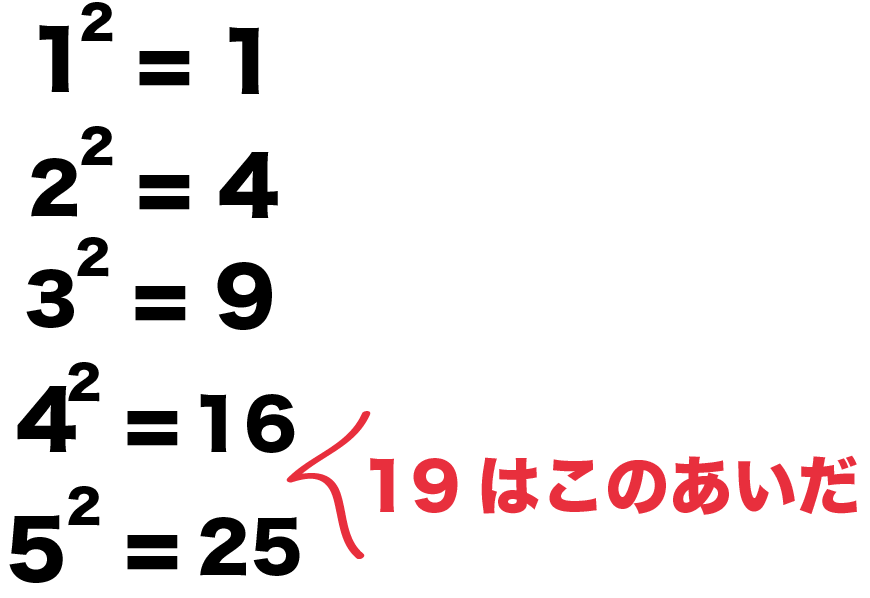



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく



平方根まとめ




中3数学 真の値と近似値の定期テスト過去問分析問題 Atstudier




高校入試調印しました 入試問題 資料の整理 近似値 Justcalm1のブログ




中学校数学自宅学習1年 資料の活用 近似値と有効数字
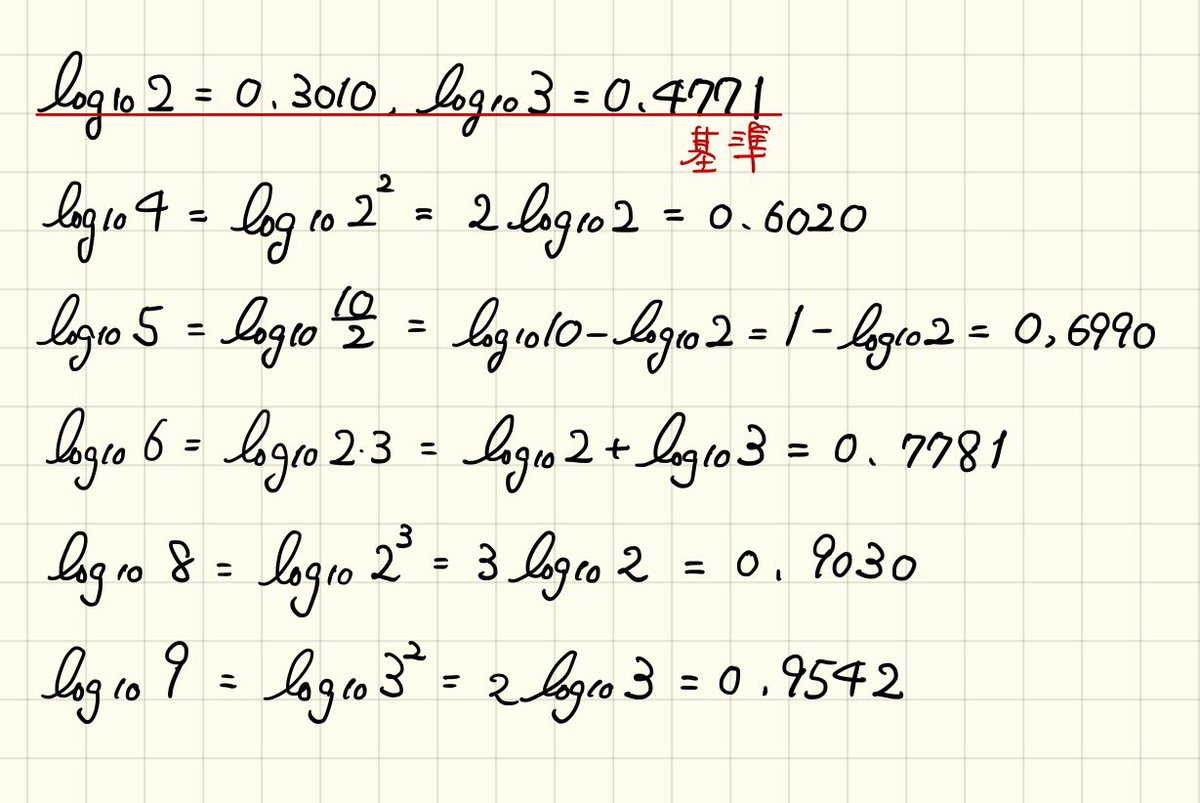



ヨビノリたくみ Twitter ನಲ ಲ 1 9の一桁の常用対数はlog7を除いてlog2とlog3の 近似 値 だけで求まるという話 数学や化学の問題で常用対数の値がこの2つしか与えられていない主な理由 特にlog5が盲点なので注意




高校数学 近似値 平方根 円周率 常用対数 自然対数の底 のゴロ合わせ 受験の月




中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




高校数学 近似値 平方根 円周率 常用対数 自然対数の底 のゴロ合わせ 受験の月
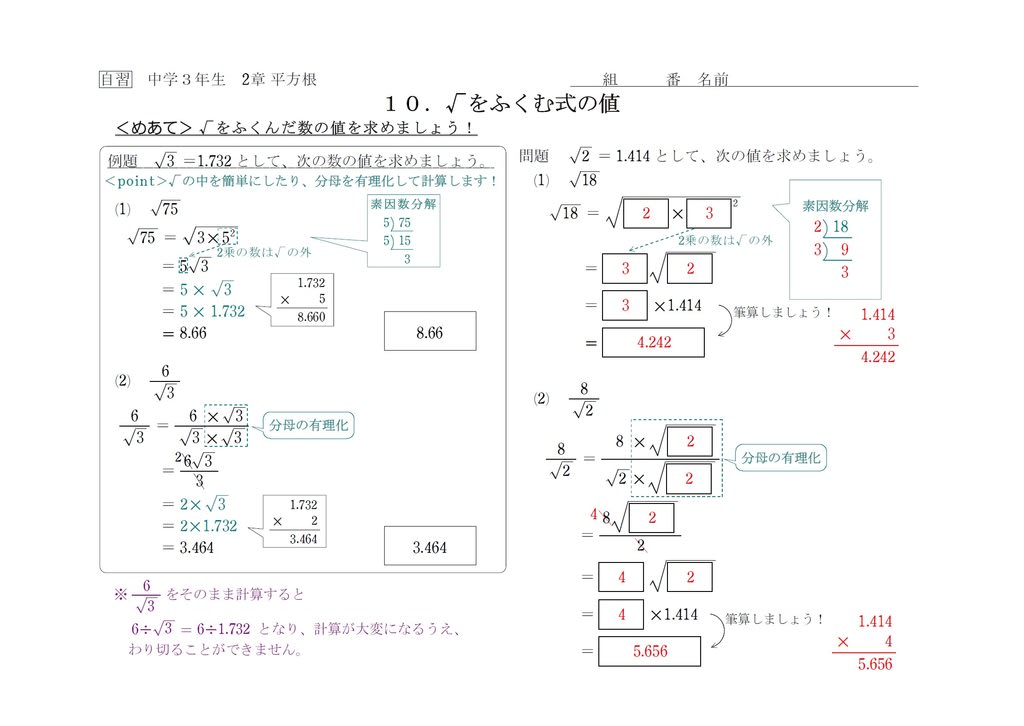



中3自習 平方根5 近似値 中学数学の勉強に




近似値と有効数字 教遊者




中3数学 平方根の近似値 例題編 映像授業のtry It トライイット




中1 数学 中1 近似値 Youtube




近似値の求め方がわかりません 解説よろしくお願いします Clear



2 のcos29 の近似値を求める問題で最後の答えが 0 8737 Yahoo 知恵袋
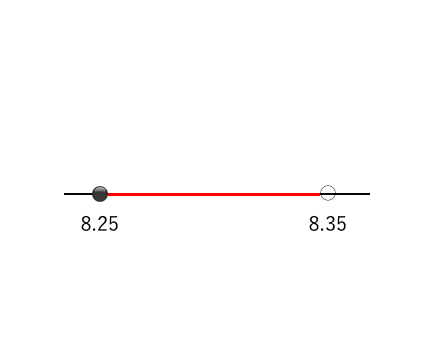



近似値の問題 苦手な数学を簡単に




高校数学 近似値の計算 問題編 映像授業のtry It トライイット




高校入試調印しました 入試問題 資料の整理 近似値 Justcalm1のブログ




中学数学 平方根 のコツ 平方根の近似値 式の値




中1数学 近似値 練習編 映像授業のtry It トライイット




中3数学 平方根の近似値の問題です Clear



1
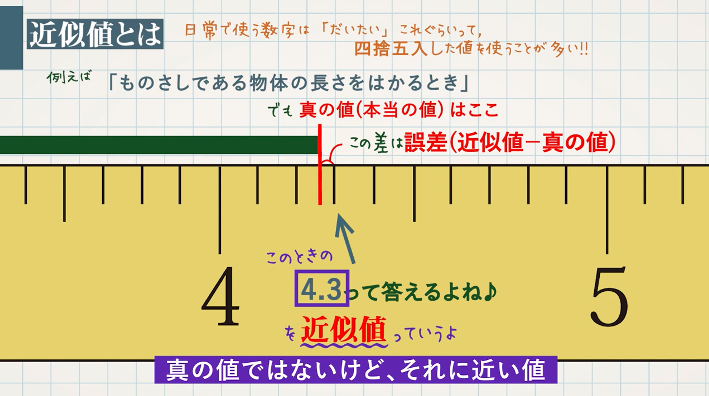



近似値と有効数字 教遊者




高校数学 近似値の計算 問題編 映像授業のtry It トライイット




中3 ルートの近似値の求め方をイチから解説 Youtube
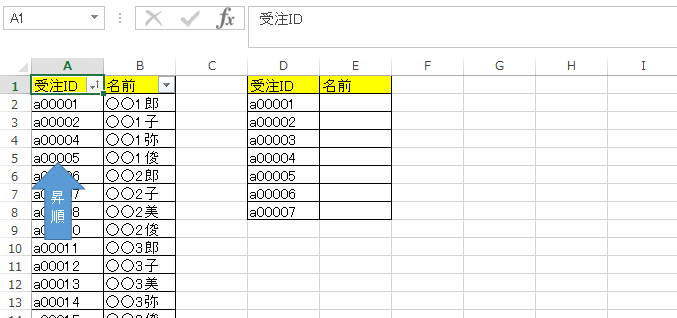



Vlookupの近似一致 近似値 あいまい検索って何に使うの




中1数学 近似値と誤差のポイントと練習問題 中学生勉強サイトあかね先生



0 件のコメント:
コメントを投稿