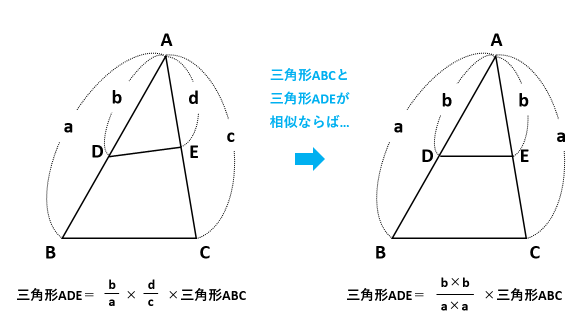
相似比と面積比 相似比と面積比① 問題(3 学期) 右の図の2 つの円a,b について,次の各問いに答えよ。 (1) a,b の円の相似比を求めよ。 (2) a,b の円の面積をそれぞれ求めよ。 (3) 面積の比を求めよ。 解答欄 (1) (2)aつまり、 相似比 \(ab\) の図形の面積の比は \(a^2b^2\) です。 なので 面積の比は \(a×ab×b\) となるわけです。 もちろん、三角形だけでなく、円や四角形や五角形やその他なんでも 相似な図形ならば、面積比は相似比の \(2\) 乗の比が成り立ちます。 例題1 三角形に限らず、どのような相似な図形においても、面積比は相似比の \(\bf{2}\) 乗となります。 相似の計算問題 それでは、ここまでに学んだ知識を活かして相似の計算問題に挑戦してみましょう。 計算問題①「三角形の相似比を求める」

Amc 10 第一讲 数学中的面积公式都是怎么来的 知乎
相似比 面積比 問題
相似比 面積比 問題-相似・線分比と面積比 レベルaの25題 問1 右の図でabとcdが平行なとき、ア〜エの長さを求めなさい。 問2 右の図でabとcdが平行なとき、ア、イ、ウの長さを求めなさい。 問3 右の図形はある土地の1:00の縮図です。この土地の実際の面積が何m2 辺の比・面積比・相似(16年東京都) 何やかんや久々の更新となりました。 今回は,典型的な難問として,辺の比や相似比を用いる問題を紹介します(問2(2))。 北海道の高校入試ではあまり見かけませんが,私立札幌第一や札幌光星,一般的な問題



相似な図形 面積比の問題 苦手な数学を簡単に
DJBは相似で相似比は3:2。 また、三角形ECDと三角形EAB は相似で相似比は1:2。 よって、AB=16cm。 三角形FGJと三角形FHBは相似 で相似比は1:2。 よってGH=8cm。 求める面積は(816)×8÷2=96cm 2 。 相似な図形の場合、 相似比を2乗して面積比を作りましょう! 面積比が分かったら、あとは楽勝だね (^^) 図形Bの面積を とおいて、比例式を作っていきましょう。 よって、図形Bの面積は ㎠ となります。 相似比の2乗だ! ってことを覚えておけば簡単です (^^) 問題 次の図において、 の面積が ㎠ であるとき、 の面積を求めなさい。 と は相似な図形にはなって 相似な図形の面積比の問題です。基本を確認して、いろいろな応用問題を解けるようにしてください。基本事項相似比が m n である図形の面積の比は,m2 n2 である。例)下のような相似な三角形がある ABCと A'B'C'の相似比は 1:2面積を求めると ABC=4 A'B'C'=16 面積比は1:4相似比が1:2のとき面積比は 12 22 となる。*立体の表面積の比も立体の相似比がm
中学受験算数「相似比と面積比」小学4年生~6年生対象毎日配信 中学受験算数「相似比と面積比」小学4年生~6年生対象毎日配信相似 面積比の問題です! なぜ aef cbfは線分の比を二乗して面積比を出しているのに、 aef abfは線分の比がそのまま面積比になるんですか? ⚠️面積比は線分の比の二乗ということは知ってます⚠️ 0 回答 ベストアンサー ブドウくん 3年以上前 面積比・・・。苦手な人多いんですよね。コツ相似比1:2 → 面積比1:4 3:5=3:a'h'だから、a'h'=5cm <問2> (2) abc=1/2×6×3=9㎝2 (1)a'b'=4a、b'c'=4b a'b'c'=1/2×10×5=25㎝2 (2)3:4 (3)面積比は、9:25 (3)9:16 まとめ 相似比1:2 →面積比1:4
相似比を2乗すれば面積比がでるってわけ。 abcと a'b'c'の相似比は、 1 2 だったね?? 面積比は2乗してやった比の、 1² 2² = 1 4 になるはず! おめでとう! 相似比から面積比を計算できちゃったね。 面積比の公式をつかった問題に挑戦! 面積比の・相似比と面積比・体積比の関係 ・線分比と面積比 について学習しました。学習内容をまとめておきますので,問題を解く前に確認しておきま しょう。 相似比と面積比・体積比の関係 1 相似比と面積比・体積比の関係 相似な図形では次のことが成り立つ。 ① 相似な図形の周の長さの比は 相似な関係にある2つの平面図形の相似比がa:bの場合、面積比はa 2 :b 2 になる という性質があります。 これがおぼえるべき、2つ目の型です。 さきほど示した17種類の内、14個は①と②をベースにしたものです。



相似三角形的性质 相似ppt 第一ppt




巧妙利用面积比等于相似比的平方比解题 哔哩哔哩 Bilibili
相似比がabのとき 面積比=(a×a)(b×b) 体積比=(a×a×a)(b×b×b) 例えば長方形の面積は「たて×横」なので、たての長さも横の長さも2倍になれば「2倍×2倍」になるという理屈です。 同じように考えて、例えば直方体の体積は「たて×横×高さ」な相似比が1:2のとき、面積比は 1 2 :2 2 になるね。 (1)の答え 面積比は1:4だから、 DEFの面積をxcm 2 とすると、中点連結定理を使った問題を解説! 相似の面積比を求める問題をイチからやってみよう! 面積比!平行四辺形の面積問題を解説!←今回の記事 面積比!台形の面積比問題を解説! 円錐の体積比を解説!




中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su




相似三角形的面積比 Isdp08am 隨意窩xuite日誌
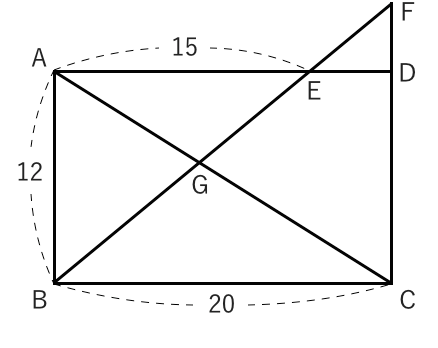
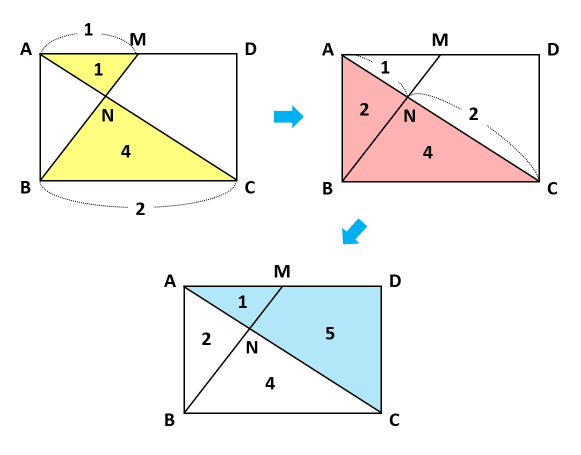
面積比の標準練習問題(解説・解答) (1)の解説 AED≡ FECより、 AGDと BGFは相似比1:2の相似となる。 よって、面積は相似比の2乗=面積比より、1:4となる。 (2)の解説 最初の公式 を利用して、今回も解くことになります。 点Bと点Eを結ぶことで利用できます。 よって、上の図示のように AGDと四角形GBCEの面積比は、2:5となります。 解答影片:例題相似三角形面積比的應用,數學 > 主題式 > 國中 > 幾何 > 相似形 > 相似三角形的應用。源自於:均一教育平台 願 每個孩子都成為終身學習者,成就自己的未來。練習問題1 以下の面積比を最も簡単な整数の比で表しなさい。 1 相似比が2:3である三角形アとイの面積の比 相似比が2:3なので、 面積比は、2 2 :3 2 =4:9 ≪答≫ 4:9




例題 相似三角形面積比的應用 數學 均一教育平台



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ
相似分野の応用問題①ラスボスっぽいの,多分それ連比です。 面積の比 (何倍)を求める問題も含めてかんたんな方法を解説します 教遊者 If playback doesn't begin shortly, try restarting your device Videos you watch may be added to the TV's watch history and influence TV recommendations To相似比と面積比についての練習です。かなり基本的な話です。 苦手な人向けです。 次回追加分は面積について計算していくものになります。 17年9月12日 画像にあるような三角形の相似に関しての長さを求める問題です。 台形については、補助線がポイントです。難易度ちょい上がりますが、いずれも基本的な内容と思います。近年の女子中で出された「平面図形」の問題の中から、今回も前回に引き続き「辺の比と面積比」の大問形式の問題を見ていきます。 前回は「高さの等しい三角形の面積」がテーマでしたが、今回は 「相似」が中心となる問題 です。 問題 右の図のように三角形abcがあり、ad:db=5:4、 ae



旋转背景下的面积比值问题 21年宜昌市中考数学第23题 腾讯网



相以三角形面积的比等于相似比的平方解决实际问题 哔哩哔哩 Bilibili
相似比の練習問題(平行四辺形4) 問6.be:da =2:3 (相似比)2 =面積比 fbe ∽ fda より fbe: fda =4:9 be:ec =2:1 底辺の比より fbe の面積: fed の面積=4:6 底辺の比より bed の面積: dec の面積=(4 +6):5「等高三角形の面積比(あるいは区切り面積)」 「隣辺比」 「相似の利用」 はその中でもよく出題される分野のひとつですから、 受講前の準備(既習範囲の知識の確認)、 受講後の復習(解法の習得と使い分け方)に取り組んで 、 「辺の比と面積比の問題はバッチリ!」 といえるように 相似な図形の体積比の問題です。基本を確認して、いろいろな応用問題を解けるようにしてください。基本事項相似比が a b である図形の面積の比は, a3 b3である。*簡単な証明もできるようにしましょう。例)1辺の長さaとbの立方体の場合相似比 → ab 体積は a3 と b3 よって上の基本



中考数学 几何综合问题中函数解析式的构造策略 附经典例题 线段



1
ただ相似図形の問題では、面積や体積の計算問題が出されることもあります。そこで、面積比や体積比がどのようになるのか理解しなければいけません。 面積比の場合、相似比の2乗になります。 例えば相似比1:2の場合、面積比は1:4(2 2 )です。相似比と面積比の関係を理解したときに「体積になったらどうなるのか」 という疑問を持たせ,次時の学習につなげましょう。 次の問題に答えなさい。 問題相似比が5:4の ABCと DEFがあります。 面積比は相似比の2乗 問題)台形abcdと三角形abeの面積比は? 1)台形なので1組は平行です。ここでは上下ですね。なのでaedとbecは相似 2)台形の「4パターン」から、相似比の二乗=面積比で以下の図になる 答え)25:6 面積比と相似:図形の面積比は相似比の2乗の中学入試問題等 問題




小学阶段三角形问题五大模型 实题实练 每日头条




相似な図形 面積比の問題 苦手な数学を簡単に
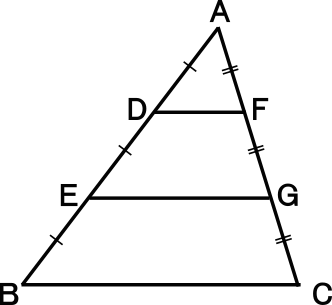
相似な図形の面積比③ 右の図の ¼abc で,点D, Eは辺 ab を3等分する点,点F,Gは辺 ac を3 等分する点である。次の問に答えなさい。 ⑴ ¼adf の面積をaとするとき,四角形 degf, 四角形 ebcg の面積を,それぞれaを使って表し なさい。 四角形 degf〔〕 四角形 ebcg〔〕 ⑵ ¼abc=54cm2 のとき,四角形 degf「相似な図形の面積比」 に関する問題を解こう。 ポイントは以下の通りだよ。 四角形でも、考え方は同じ だよ。さらに,相似な図形の相似比と面積比,体積 比の関係など相似な図形の計量に関する学習を通して,相似な図形の理解をさらに深めるとともに, 数学のよさを体験させながら数学的な推論に関する能力,図形について見通しをもって論理的に考察 する能力を伸ばしていきたい。 (2) 生徒観 本



数学i Aチェック リピート 第4章 2図形への応用 8 相似形の面積比 Pukiwiki



数学 相似三角形系列03 面积比问题
相似比2 =面積比より dgf: cef =16:25 ag:gf =6:4 となるので 高さの等しい三角形の面積は, 底辺の比=面積比より dgf: adg =16:24 したがって adf: fec =40:25 =8:5 問2. (ア)bd =dc,ae:ec =2:1 ae:gb =2:3 =ef:fb abf: afe =6:4長さの比は相似比と同じ。 面積比は相似比の2乗。 体積比は相似比の3乗。 相似比がabの相似な図形の場合 辺、高さなど 長さの比は a b 表面積など 面積比は a 2 b 2 体積比は a 3 b 3 例 相似比23の相似な円柱PとQがある。 2h 2r 3r 3h今問題文で辺の比が与えられていて、求めるのは三角形の面積比→ということは辺の比と面積比の関係を思い浮かべる→すると相似の三角形では相似 比の 2 乗が面積比となることがわかっている。



相似三角形的面積比與邊長對應關係比 Live 多媒體數學觀念典online




初中數學相似三角形的判定定理證明及利用三角形相似解決問題 每日頭條
相似比と面積比,体積比の公式の証明 レベル ★ 基礎 平面図形 更新日時 相似な平面図形について,面積比=相似比の二乗 相似な空間図形について,体積比=相似比の三乗 面積比をきちんと理解できれば体積比もほぼ同様に理解できるので




几何问题之相似三角形 网易订阅




難関中学に合格する 相似形と面積比 図形の移動トレーニング 賛数仙人の教え Amazon Com Books



この問題の面積比のだし方を教えてください 相似比の二乗じゃないですよ Yahoo 知恵袋
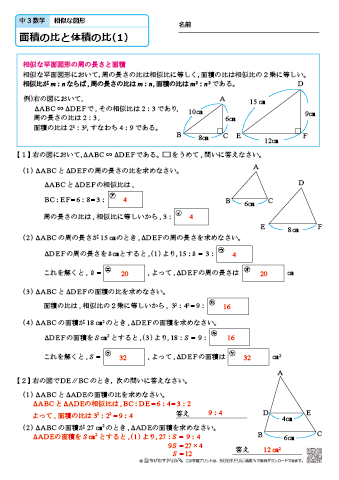



中学3年生 数学 面積の比と体積の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




相似 平行四辺形と面積比の問題を徹底解説 数スタ
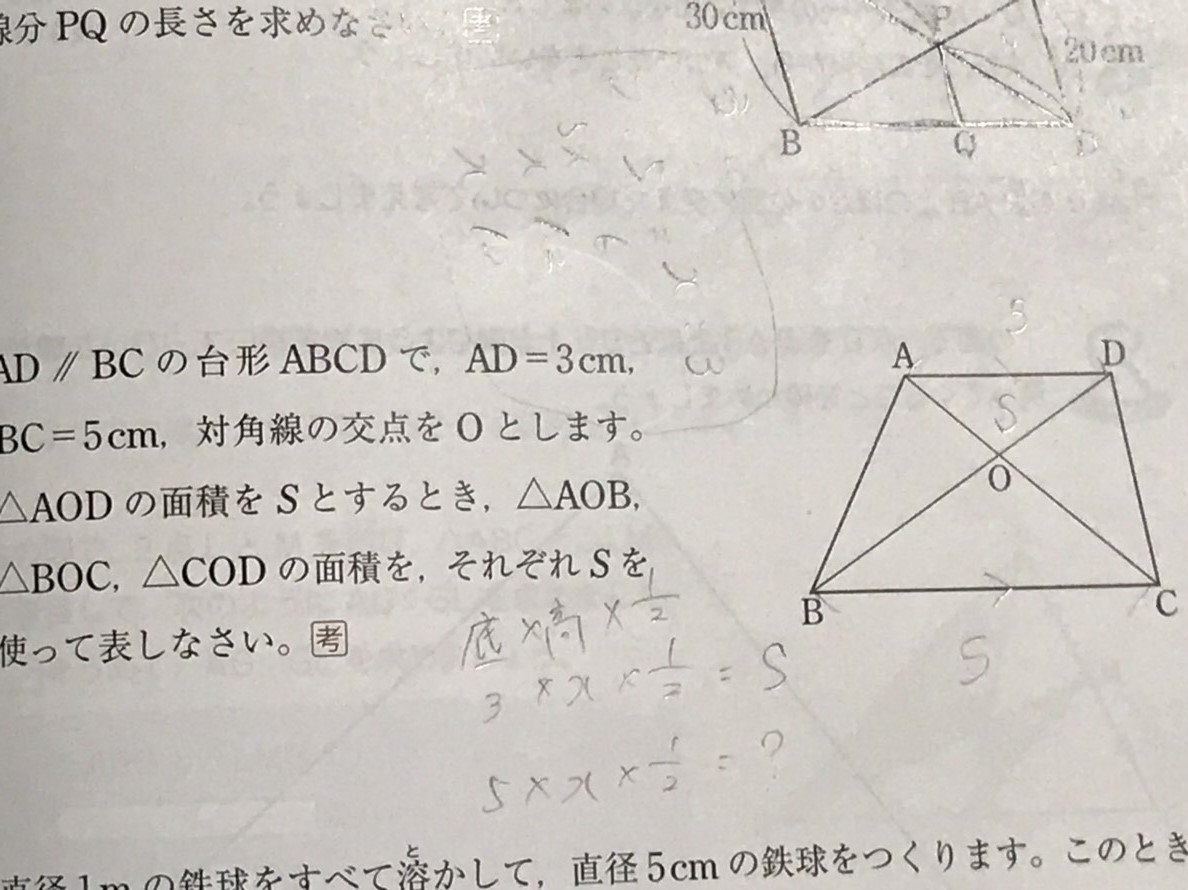



面積比



数学 相似三角形系列03 面积比问题




辺の比と面積比問題 考え方1 Youtube




相似多边形的性质 Ppt课件下载 Ppt模板 爱问共享资料



数学 相似三角形系列03 面积比问题




相似三角形的周长和面积导学案下载 Word模板 爱问共享资料




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学




三角度等于多少啊 一个三角形是多少度 三人行教育网 Www 3rxing Org




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学




数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




Amc 10 第一讲 数学中的面积公式都是怎么来的 知乎



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




相似三角形的周长和面积下载 Word模板 爱问共享资料
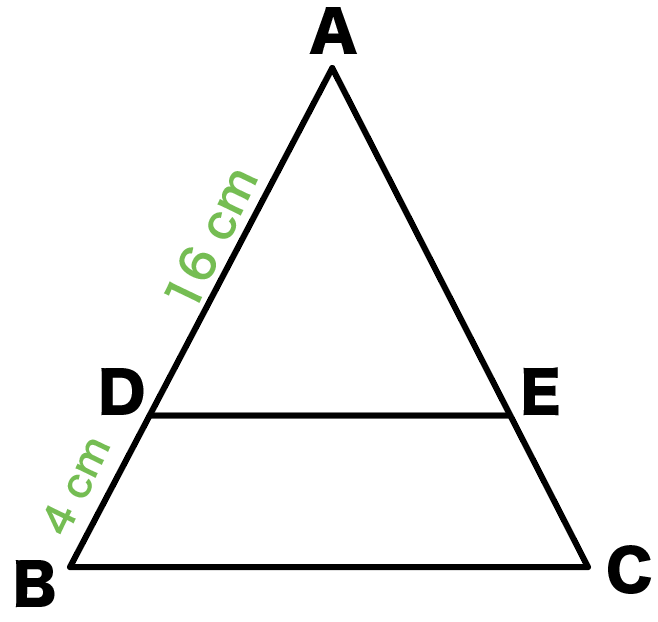



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく




九年级数学上册23 3 相似三角形23 3 3 相似三角形的性质导学案华东师大版下载 Word模板 爱问共享资料




相似の面積比を求める問題 上級編 Youtube
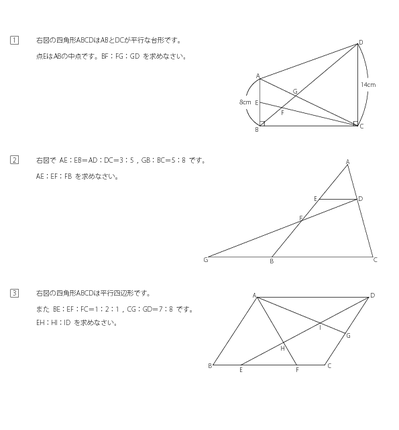



みんなの算数オンライン 中学受験5年 相似比と面積比3 相似の利用1



第四章相似形 图片欣赏中心 急不急图文 Jpjww Com




ベスト中3 数学相似 最高のカラーリングのアイデア



面積比問題より 相似比の間違い これが中学入試に出た図形問題



27 2 3相似三角形的周长与面积 新人教版九年级下 下载 Word模板 爱问共享资料




小学阶段三角形问题五大模型 实题实练 每日头条



相似三角形的问题 图片欣赏中心 急不急图文 Jpjww Com
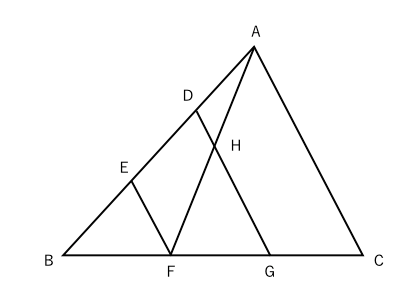



面積が何倍かを求める問題 応用編 苦手な数学を簡単に



4 7 第2课时相似三角形的周长和面积之比 免费资源共享课件巴巴www Kejian Com公众号kejianbaba打包 Ppt 课件巴巴kejian Com 课件巴巴kejian Com




例題 梯形的兩對角線與相似形 Youtube
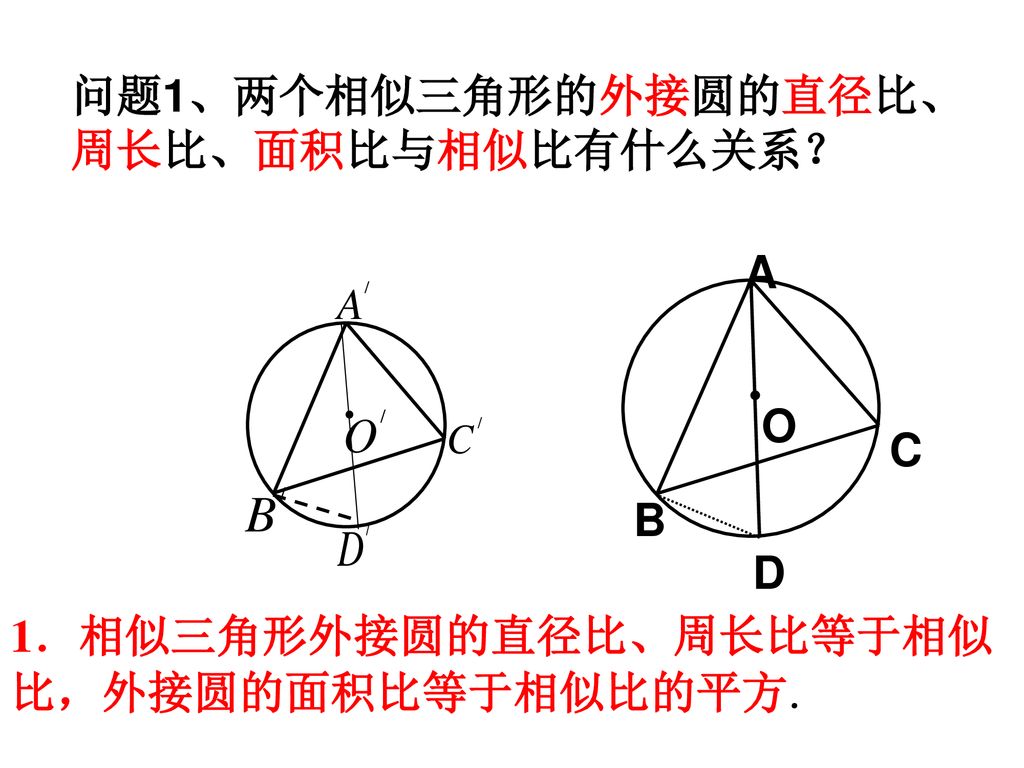



相似三角形的判定 1 Ppt Download




等高三角形面積比 Youtube



打印预览
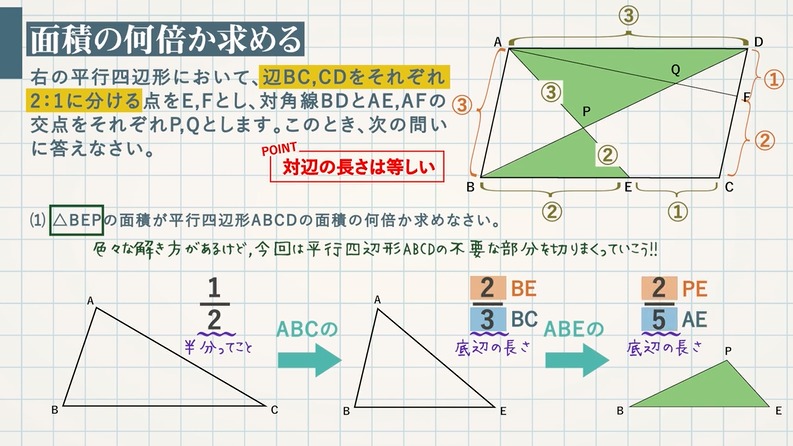



相似分野の応用問題 ラスボスっぽいの 多分それ連比です 面積の比 何倍 を求める問題も含めてかんたんな方法を解説します 教遊者




三角形の面積比と相似比 チーム エン




相似比と面積比 中学3年数学 Youtube



数学 相似三角形系列03 面积比问题




相似三角形的判定 1 Ppt Download



相似三角形的性质 相似ppt 第一ppt




相似比 搜索结果 哔哩哔哩 Bilibili



相似三角形的性质 图形的相似ppt 第2课时 第一ppt




周長 面積 比 在平面幾何問題中的巧用 每日頭條



比例线段 相似三角模型比例线段




15秋湘教版数学九上3 4 2 相似三角形的性质 Word教案下载 Word模板 爱问共享资料




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学




数学相似三角形知识点 相似三角形的性质和判定 星火网校



218几何原本第六卷 命题19 相似三角形面积的比等于相似比的平方 哔哩哔哩 つロ干杯 Bilibili




相似三角形的面積比 Isdp08am 隨意窩xuite日誌



相似三角形的性质 新授课 数学错题本 微信公众号文章阅读 Wemp



中学3年数学練習問題 相似な平面図形の面積の比 図形と相似




ベスト中3 数学相似 最高のカラーリングのアイデア




高校入試対策数学 面積比に関する対策問題 Pikuu




平面図形の苦手を解消 三角形の面積比 基本編




相似じゃない三角形の面積比の求め方がよく分かりません Clear
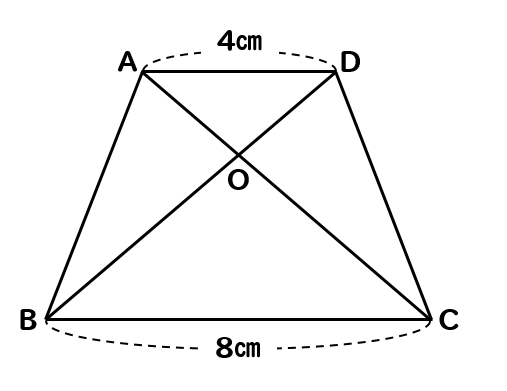



相似 台形と面積比の問題を徹底解説 数スタ
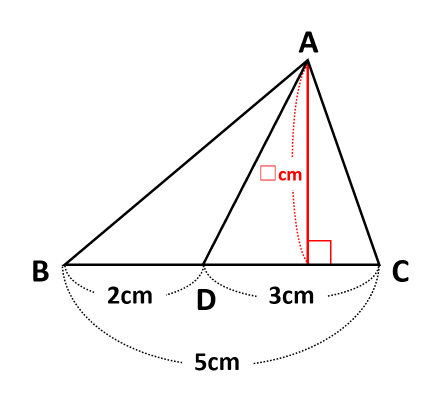



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ



初中数学方法与技巧 特殊四边形中的面积比问题 复习



1




数学 中3 53 相似と面積 応用編 Youtube



三角形的性质 万图壁纸网
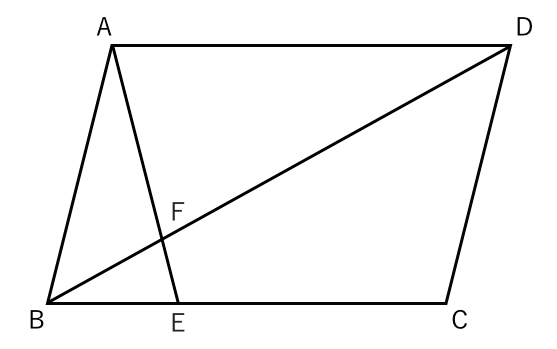



相似な図形 面積比の問題 苦手な数学を簡単に




4 7相似三角形的周长和面积之比 第2课时 课件 七七文库www 77wenku Com




Ppt 相似形與sss 相似性質powerpoint Presentation Free Download Id



相似三角形的性质 新授课 数学错题本 微信公众号文章阅读 Wemp



4 7相似三角形的周长和面积之比 第2课时 课件 七七文库www 77wenku Com



数学 相似三角形系列03 面积比问题



相似三角形的性质 相似ppt 第一ppt
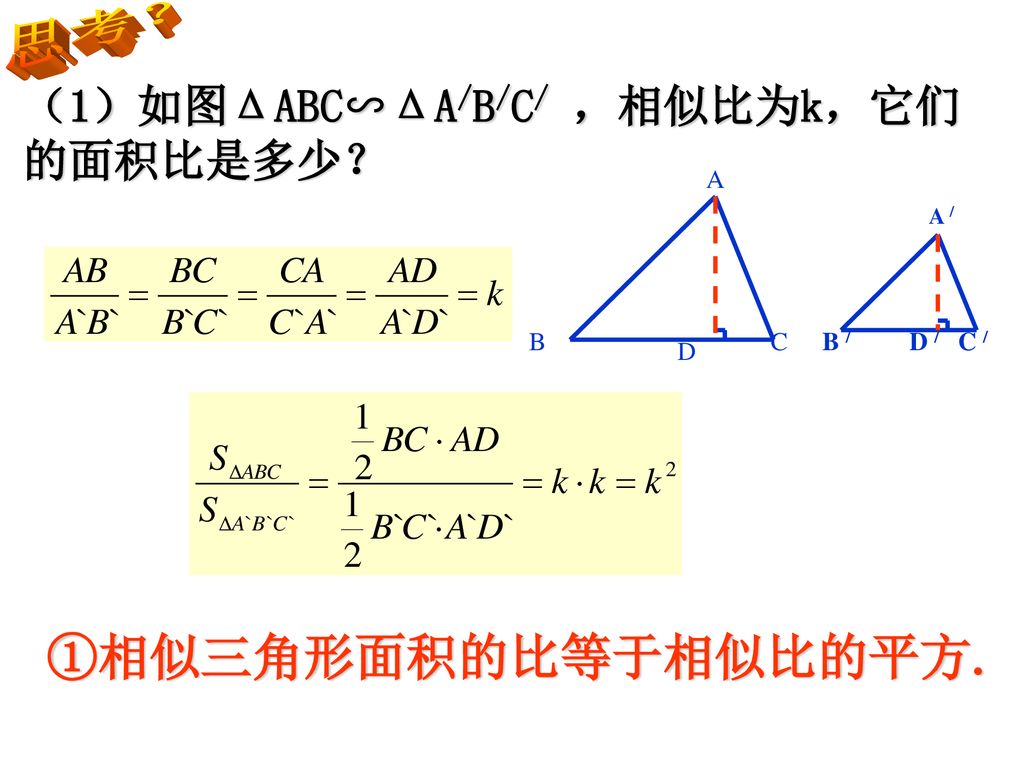



27 2 3相似三角形的周长与面积 Ppt Download
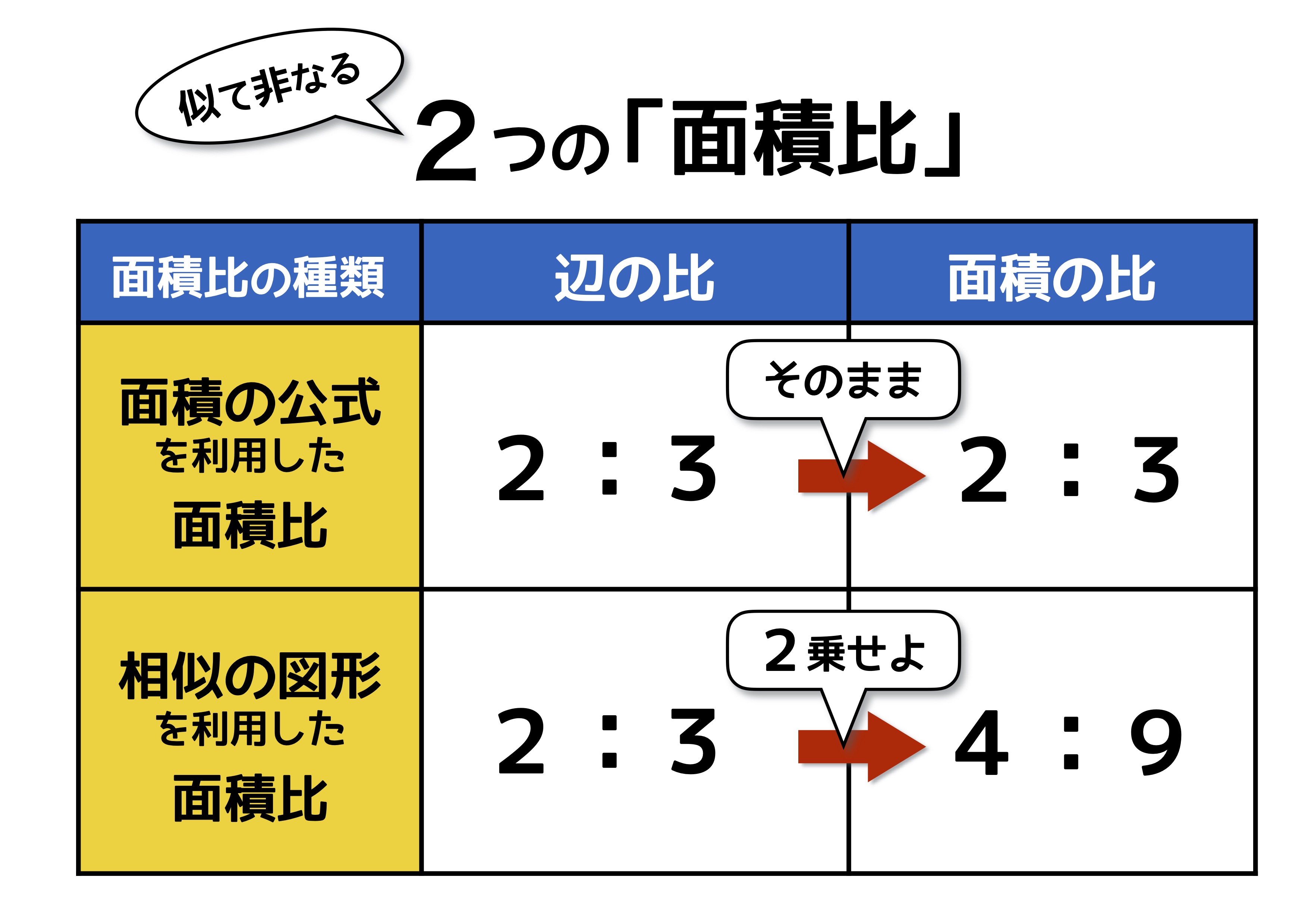



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



相以三角形面积的比等于相似比的平方解决实际问题 哔哩哔哩 Bilibili



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ



1




相似な図形の面積比 問題 Youtube




平面図形をマスター 三角形の面積比 応用編その2
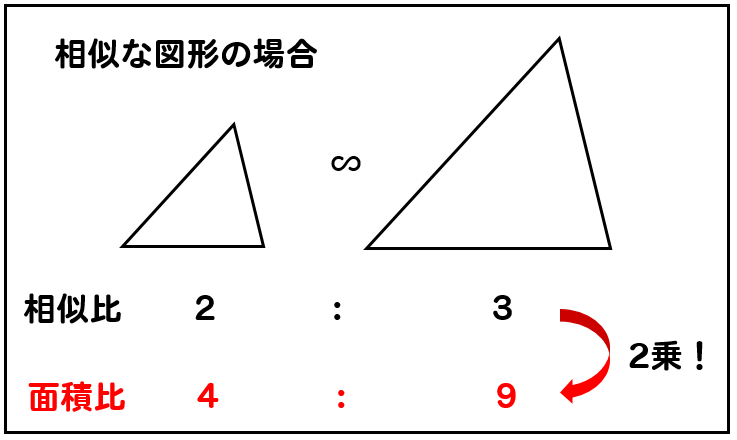



これでバッチリ 相似の面積比を求める問題をイチからやってみよう 数スタ




微博搜索



面积比问题1 哔哩哔哩 つロ干杯 Bilibili



打印预览




中学数学 相似じゃない面積比 平面図形 Youtube



4 4相似三角形的性质极其应用一 Ppt 沃文网wodocx Com



相似的性质 全等三角形的性质 北京在明律师事务所



1




相似な図形の面積比の問題 相似比を出してから二乗しよう 中学や高校の数学の計算問題




三角に関する質問 68ページ 勉強質問サイト
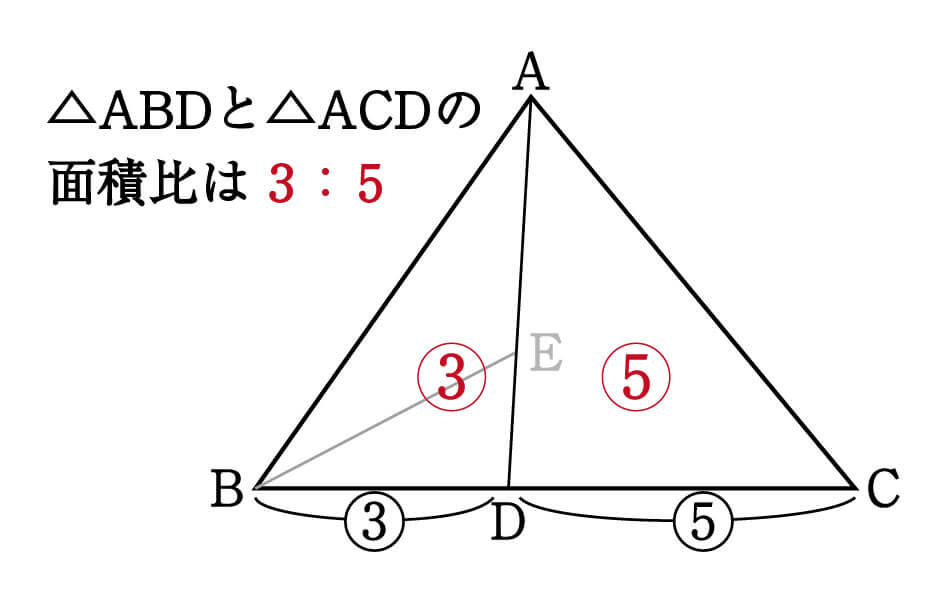



数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
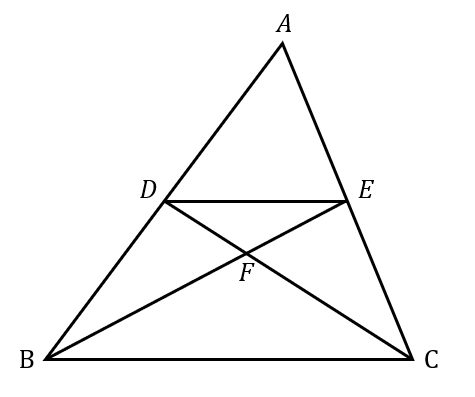



これでバッチリ 相似の面積比を求める問題をイチからやってみよう 数スタ
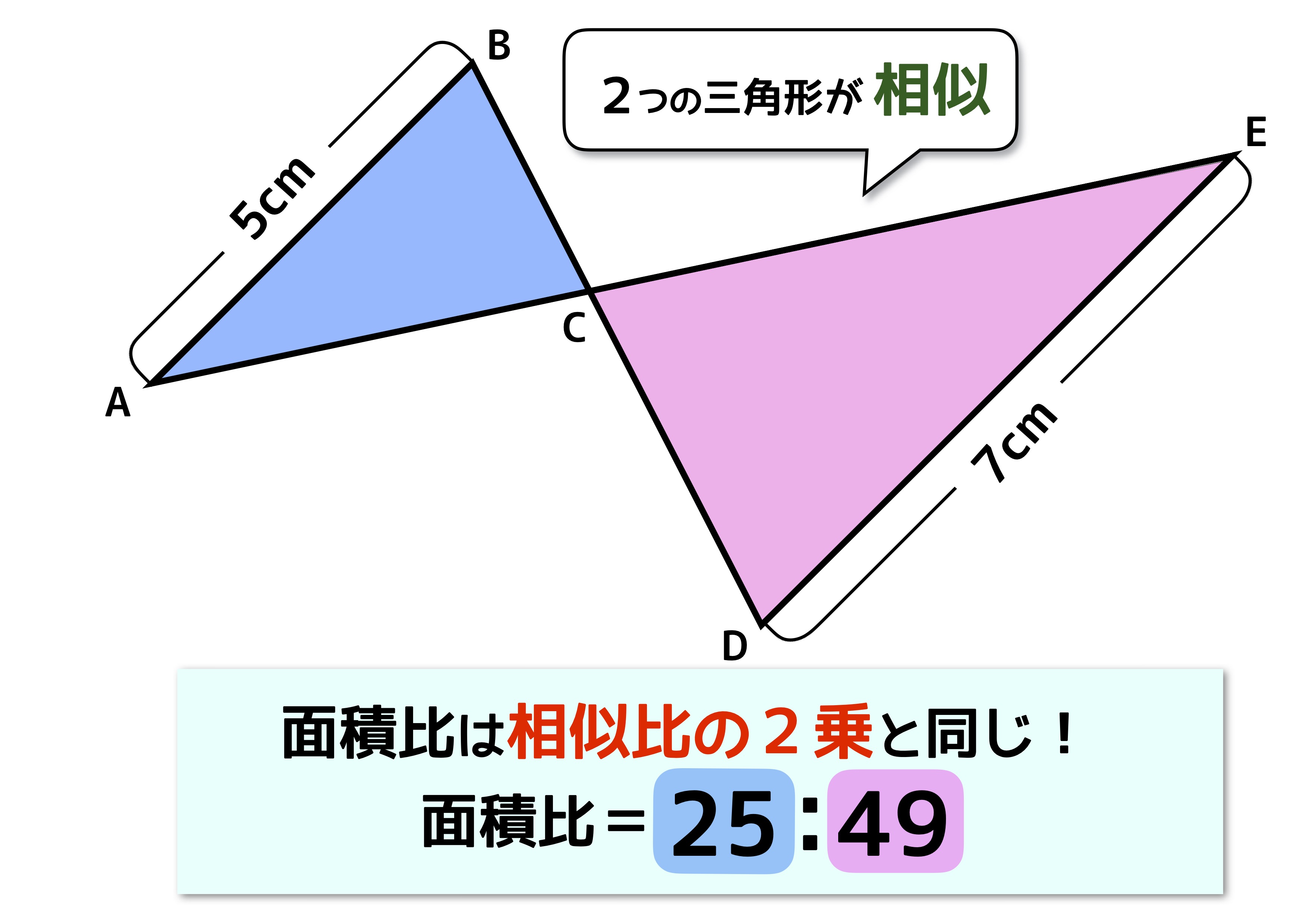



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



0 件のコメント:
コメントを投稿